Dive into the fundamentals of perceptrons, the foundational concept that led to the development of neural networks, and learn how to implement one in Python.
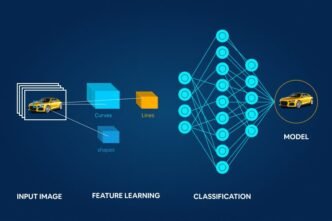
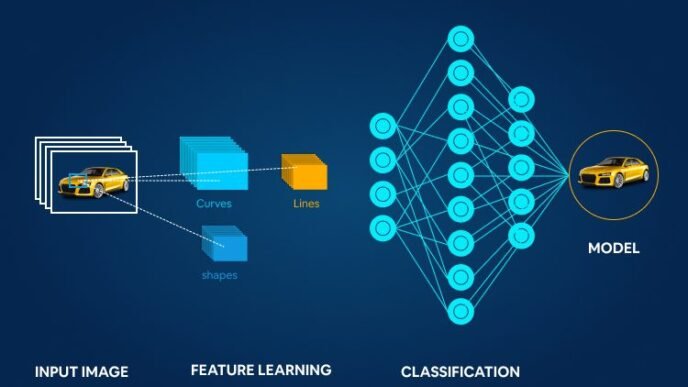
Machine learning models have evolved into sophisticated systems, but their journey began with something simple: the perceptron. This fundamental building block of artificial neural networks laid the groundwork for complex deep learning models. In this article, we’ll explore what a perceptron is, how it works, its limitations, and what alternatives are available today.
1. What is a Perceptron?
A perceptron is one of the earliest types of artificial neurons, introduced by Frank Rosenblatt in the late 1950s. It mimics a biological neuron, processing input data and outputting a decision. Essentially, a perceptron takes multiple inputs, applies weights, sums them, and then passes the result through an activation function to produce a binary output—either 0 or 1. This basic structure is a stepping stone toward understanding more complex neural networks.
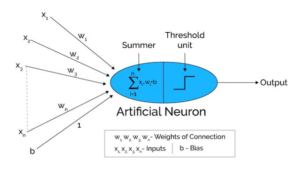
Key Components of a Perceptron:
- Inputs (Features): The input data points, which the perceptron evaluates.
- Weights: Each input has a corresponding weight that determines its importance.
- Bias: An additional parameter that allows the perceptron to fit the data better.
- Activation Function: The function that determines the output based on the weighted sum of inputs.
2. The Perceptron Algorithm: How Does It Work?
The perceptron algorithm learns by adjusting weights iteratively. Here’s a breakdown of how the algorithm works:
- Initialize Weights and Bias: Start with small random weights and a bias term.
- Calculate the Output: For each input, calculate the weighted sum and pass it through an activation function (often a step function).
- Compare Output with Expected Value: If the output differs from the actual label, update the weights.
- Repeat: Continue this process until the model achieves acceptable accuracy.
This iterative learning is known as “gradient descent” and allows the perceptron to minimize its prediction error over time.
3. Implementing a Perceptron in Python
Here’s a basic Python implementation of a single-layer perceptron to classify data points.
import numpy as np
class Perceptron:
def __init__(self, learning_rate=0.01, epochs=1000):
self.learning_rate = learning_rate
self.epochs = epochs
self.weights = None
self.bias = None
def _activation_function(self, x):
return 1 if x >= 0 else 0
def fit(self, X, y):
# Initialize weights and bias
self.weights = np.zeros(X.shape[1])
self.bias = 0
for _ in range(self.epochs):
for idx, x_i in enumerate(X):
linear_output = np.dot(x_i, self.weights) + self.bias
y_predicted = self._activation_function(linear_output)
# Calculate the error
error = y[idx] - y_predicted
# Update weights and bias
self.weights += self.learning_rate * error * x_i
self.bias += self.learning_rate * error
def predict(self, X):
linear_output = np.dot(X, self.weights) + self.bias
return [self._activation_function(x) for x in linear_output]
# Example usage
X = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
y = np.array([1, 0, 0, 0]) # AND gate example
perceptron = Perceptron(learning_rate=0.1, epochs=10)
perceptron.fit(X, y)
predictions = perceptron.predict(X)
print("Predictions:", predictions)
This code demonstrates a perceptron trained to model an AND gate, a simple logical operation. Adjust the learning_rate and epochs to fine-tune the model’s performance.